
Содержание
Алгоритм шифрования Магма представляет собой точную копию алгоритма блочного шифрования из старого ГОСТ 28147—89, за одним исключением. В новом ГОСТ 34.12—2015 определена и задана таблица перестановок для нелинейного биективного преобразования, которая в старом ГОСТ 28147—89 отсутствовала, и задание ее элементов полностью отдавалось в руки людей, реализующих данный алгоритм. Теоретически, если определить элементы таблицы перестановок самостоятельно и сохранить таблицу в тайне, это позволит увеличить стойкость алгоритма шифрования (за счет этого фактически увеличивается длина ключа), однако, как видим, разработчики ГОСТ 34.12—2015 решили лишить самостоятельности пользователей стандарта.
Как уже было сказано, длина шифруемого блока в алгоритме «Магма» — 64 бита. Длина ключа шифрования — 256 бит.
Еще по теме: PGP / GPG шифрование
Немного теории о шифровании Магма
В описываемом алгоритме блок, подлежащий зашифровыванию (напомню, его длина 64 бита), разделяется на две равные по длине (32 бита) части — правую и левую. Далее выполняется тридцать две итерации с использованием итерационных ключей, получаемых из исходного 256-битного ключа шифрования.
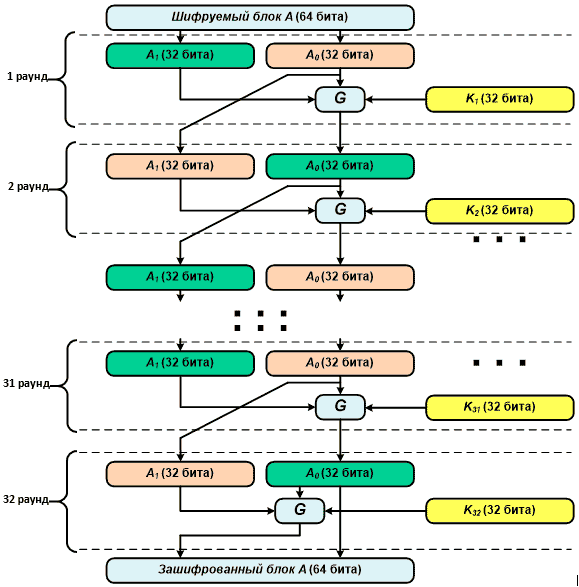
Во время каждой итерации (за исключением тридцать второй) с правой и левой половиной зашифровываемого блока производится одно преобразование, основанное на сети Фейстеля. Сначала правая часть складывается по модулю 32 с текущим итерационным ключом, затем полученное 32-битное число делится на восемь 4-битных и каждое из них с использованием таблицы перестановки преобразуется в другое 4-битное число (если помнишь, то в предыдущих двух статьях это называлось нелинейным биективным преобразованием). После этого преобразования полученное число циклически сдвигается влево на одиннадцать разрядов. Далее результат ксорится с левой половиной блока. Получившееся 32-битное число записывается в правую половину блока, а старое содержимое правой половины переносится в левую половину блока.
В ходе последней (тридцать второй) итерации так же, как описано выше, преобразуется правая половина, после чего полученный результат пишется в левую часть исходного блока, а правая половина сохраняет свое значение.
Итерационные ключи получаются из исходного 256-битного ключа. Исходный ключ делится на восемь 32-битных подключей, и далее они используются в следующем порядке: три раза с первого по восьмой и один раз с восьмого по первый.

Для расшифровывания используется такая же последовательность итераций, как и при зашифровывании, но порядок следования ключей изменяется на обратный.

Итак, после краткого и небольшого погружения в теорию начинаем кодить…
Базовые функции стандарта шифрования Магма
Поскольку в алгоритме используются 32-битные блоки (в виде так называемых двоичных векторов), для начала определим этот самый блок:
|
1 2 3 4 5 |
// Размер блока 4 байта (или 32 бита) #define BLOCK_SIZE 4 ... // Определяем тип vect как 4-байтовый массив typedef uint8_t vect[BLOCK_SIZE]; |
Сложение двух двоичных векторов по модулю 2
Каждый байт первого вектора ксорится с соответствующим байтом второго вектора, и результат пишется в третий (выходной) вектор:
|
1 2 3 4 5 6 |
static void GOST_Magma_Add(const uint8_t *a, const uint8_t *b, uint8_t *c) { int i; for (i = 0; i < BLOCK_SIZE; i++) c[i] = a[i]^b[i]; } |
Сложение двух двоичных векторов по модулю 32
Данная функция аналогична функции под названием «сложение в кольце вычетов по модулю 2 в степени n» из алгоритма «Стрибог», за исключением того, что n в нашем случае будет равно 32, а не 512, как в стандарте «Стрибог». Два исходных 4-байтовых вектора представляются как два 32-битных числа, далее они складываются, переполнение, если оно появляется, отбрасывается:
|
1 2 3 4 5 6 7 8 9 10 |
static void GOST_Magma_Add_32(const uint8_t *a, const uint8_t *b, uint8_t *c) { int i; unsigned int internal = 0; for (i = 3; i >= 0; i--) { internal = a[i] + b[i] + (internal >> 8); c[i] = internal & 0xff; } } |
Нелинейное биективное преобразование (преобразование T)
В отличие от алгоритмов «Стрибог» и «Кузнечик» (кстати, там это преобразование называется S-преобразованием) таблица перестановок здесь используется другая:
|
1 2 3 4 5 6 7 8 9 10 11 |
static unsigned char Pi[8][16]= { {1,7,14,13,0,5,8,3,4,15,10,6,9,12,11,2}, {8,14,2,5,6,9,1,12,15,4,11,0,13,10,3,7}, {5,13,15,6,9,2,12,10,11,7,8,1,4,3,14,0}, {7,15,5,10,8,1,6,13,0,9,3,14,11,4,2,12}, {12,8,2,1,13,4,15,6,7,0,10,5,3,14,9,11}, {11,3,5,8,2,15,10,13,14,1,7,4,12,9,6,0}, {6,8,2,3,9,10,5,12,1,14,4,7,11,13,0,15}, {12,4,6,2,10,5,11,9,14,8,13,7,0,3,15,1} }; |
Поскольку в тексте стандарта (по неведомой традиции) нулевой байт пишется в конце, а последний в начале, то для корректной работы программы строки таблицы необходимо записывать в обратном порядке, а не так, как изложено в стандарте.
Код самой функции преобразования T получается такой:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
static void GOST_Magma_T(const uint8_t *in_data, uint8_t *out_data) { uint8_t first_part_byte, sec_part_byte; int i; for (i = 0; i < 4; i++) { // Извлекаем первую 4-битную часть байта first_part_byte = (in_data[i] & 0xf0) >> 4; // Извлекаем вторую 4-битную часть байта sec_part_byte = (in_data[i] & 0x0f); // Выполняем замену в соответствии с таблицей подстановок first_part_byte = Pi[i * 2][first_part_byte]; sec_part_byte = Pi[i * 2 + 1][sec_part_byte]; // «Склеиваем» обе 4-битные части обратно в байт out_data[i] = (first_part_byte << 4) | sec_part_byte; } } |
Развертывание ключей
В начале мы уже говорили, что для зашифровывания и расшифровывания нам нужно тридцать два итерационных 32-битных ключа, которые получаются из исходного 256-битного.
Для начала определим место, где будут храниться полученные значения ключей:
|
1 |
vect iter_key[32]; // Итерационные ключи шифрования |
После чего можно заняться непосредственным развертыванием ключей:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
void GOST_Magma_Expand_Key(const uint8_t *key) { // Формируем восемь 32-битных подключей в порядке следования с первого по восьмой memcpy(iter_key[0], key, 4); memcpy(iter_key[1], key + 4, 4); memcpy(iter_key[2], key + 8, 4); memcpy(iter_key[3], key + 12, 4); memcpy(iter_key[4], key + 16, 4); memcpy(iter_key[5], key + 20, 4); memcpy(iter_key[6], key + 24, 4); memcpy(iter_key[7], key + 28, 4); ... // Повторяем предыдущий кусочек кода еще два раза ... // Формируем восемь 32-битных подключей в порядке следования с восьмого по первый memcpy(iter_key[24], key + 28, 4); memcpy(iter_key[25], key + 24, 4); memcpy(iter_key[26], key + 20, 4); memcpy(iter_key[27], key + 16, 4); memcpy(iter_key[28], key + 12, 4); memcpy(iter_key[29], key + 8, 4); memcpy(iter_key[30], key + 4, 4); memcpy(iter_key[31], key, 4); } |

Все это, конечно, можно написать с использованием циклов, но в данном случае эта функция реализована, так сказать, «в лоб» для наглядности, да и работать она в таком виде теоретически должна быстрее.
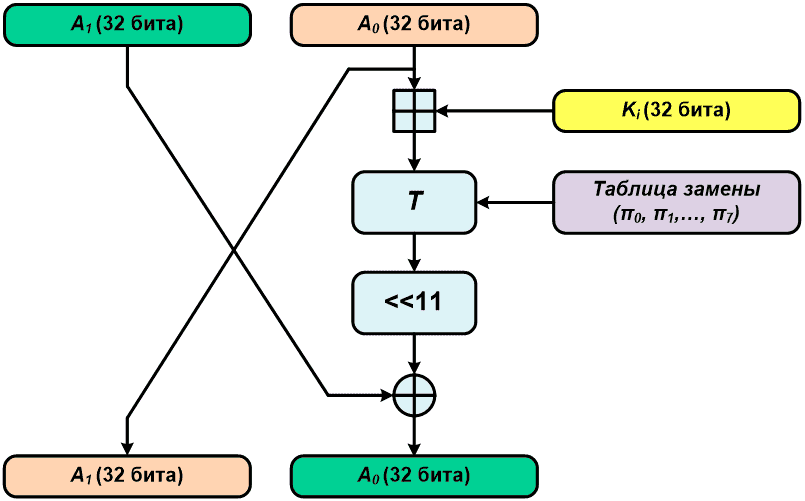
Преобразование g
Это преобразование включает в себя сложение правой части блока с итерационным ключом по модулю 32, нелинейное биективное преобразование и сдвиг влево на одиннадцать разрядов:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
static void GOST_Magma_g(const uint8_t *k, const uint8_t *a, uint8_t *out_data) { uint8_t internal[4]; uint32_t out_data_32; // Складываем по модулю 32 правую половину блока с итерационным ключом GOST_Magma_Add_32(a, k, internal); // Производим нелинейное биективное преобразование результата GOST_Magma_T(internal, internal); // Преобразовываем четырехбайтный вектор в одно 32-битное число out_data_32 = internal[0]; out_data_32 = (out_data_32 << 8) + internal[1]; out_data_32 = (out_data_32 << 8) + internal[2]; out_data_32 = (out_data_32 << 8) + internal[3]; // Циклически сдвигаем все влево на 11 разрядов out_data_32 = (out_data_32 << 11)|(out_data_32 >> 21); // Преобразовываем 32-битный результат сдвига обратно в 4-байтовый вектор out_data[3] = out_data_32; out_data[2] = out_data_32 >> 8; out_data[1] = out_data_32 >> 16; out_data[0] = out_data_32 >> 24; } |
Преобразование G
Это преобразование представляет собой одну итерацию цикла зашифровывания или расшифровывания (с первой по тридцать первую). Включает в себя преобразование g, сложение по модулю 2 результата преобразования g с правой половиной блока и обмен содержимым между правой и левой частью блока:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
static void GOST_Magma_G(const uint8_t *k, const uint8_t *a, uint8_t *out_data) { uint8_t a_0[4]; // Правая половина блока uint8_t a_1[4]; // Левая половина блока uint8_t G[4]; int i; // Делим 64-битный исходный блок на две части for(i = 0; i < 4; i++) { a_0[i] = a[4 + i]; a_1[i] = a[i]; } // Производим преобразование g GOST_Magma_g(k, a_0, G); // Ксорим результат преобразования g с левой половиной блока GOST_Magma_Add(a_1, G, G); for(i = 0; i < 4; i++) { // Пишем в левую половину значение из правой a_1[i] = a_0[i]; // Пишем результат GOST_Magma_Add в правую половину блока a_0[i] = G[i]; } // Сводим правую и левую части блока в одно целое for(i = 0; i < 4; i++) { out_data[i] = a_1[i]; out_data[4 + i] = a_0[i]; } } |
Финальное преобразование G
Это последняя (тридцать вторая) итерация цикла зашифровывания или расшифровывания. От простого преобразования G отличается отсутствием обмена значениями между правой и левой частью исходного блока:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
static void GOST_Magma_G_Fin(const uint8_t *k, const uint8_t *a, uint8_t *out_data) { uint8_t a_0[4]; // Правая половина блока uint8_t a_1[4]; // Левая половина блока uint8_t G[4]; int i; // Делим 64-битный исходный блок на две части for(i = 0; i < 4; i++) { a_0[i] = a[4 + i]; a_1[i] = a[i]; } // Производим преобразование g GOST_Magma_g(k, a_0, G); // Ксорим результат преобразования g с левой половиной блока GOST_Magma_Add(a_1, G, G); // Пишем результат GOST_Magma_Add в левую половину блока for(i = 0; i < 4; i++) a_1[i] = G[i]; // Сводим правую и левую части блока в одно целое for(i = 0; i < 4; i++) { out_data[i] = a_1[i]; out_data[4 + i] = a_0[i]; } } |
Шифрование Магма
Как мы уже говорили, шифрование производится путем тридцати двух итераций, с первой по тридцать первую с применением преобразования G и тридцать вторую с применением финального преобразования G:
|
1 2 3 4 5 6 7 8 9 10 11 |
void GOST_Magma_Encript(const uint8_t *blk, uint8_t *out_blk) { int i; // Первое преобразование G GOST_Magma_G(iter_key[0], blk, out_blk); // Последующие (со второго по тридцать первое) преобразования G for(i = 1; i < 31; i++) GOST_Magma_G(iter_key[i], out_blk, out_blk); // Последнее (тридцать второе) преобразование G GOST_Magma_G_Fin(iter_key[31], out_blk, out_blk); } |
Перед запуском данной функции не забудь вызвать GOST_Magma_ExpandKey, чтобы заполнить массив с итерационными ключами нужными значениями.
Расшифровывание Магма
Расшифровывание выполняется аналогично зашифровыванию с использованием итерационных ключей в обратном порядке:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
void GOST_Magma_Decript(const uint8_t *blk, uint8_t *out_blk) { int i; // Первое преобразование G с использованием // тридцать второго итерационного ключа GOST_Magma_G(iter_key[31], blk, out_blk); // Последующие (со второго по тридцать первое) преобразования G // (итерационные ключи идут в обратном порядке) for(i = 30; i > 0; i--) GOST_Magma_G(iter_key[i], out_blk, out_blk); // Последнее (тридцать второе) преобразование G // с использованием первого итерационного ключа GOST_Magma_G_Fin(iter_key[0], out_blk, out_blk); } |
Здесь также не стоит забывать про GOST_Magma_ExpandKey, так как для расшифровывания используются те же итерационные ключи, что и для зашифровывания.

Заключение
Алгоритм «Магма» из ГОСТ 34.12—2015 гораздо проще реализуется по сравнению с алгоритмом «Кузнечик» из того же ГОСТа, при этом на сегодняшний день он гораздо чаще используется (в том числе и в варианте ГОСТ 28147—89 с таблицами замены, определяемыми разработчиками самостоятельно или руководствуясь методическим документом RFC 4357).
Теперь ты можешь шифровать как 128-разрядные блоки (алгоритмом «Кузнечик»), так и 64-разрядные (алгоритмом «Магма»). Процедуры шифрования больших объемов, а также режимы работы (а именно режим простой замены, режим гаммирования, режим гаммирования с обратной связью по выходу, режим простой замены с зацеплением, режим гаммирования с обратной связью по шифртексту и режим выработки имитовставки) этих двух алгоритмов изложены в другом нормативном документе: ГОСТ 34.13—2015 «Информационная технология. Криптографическая защита информации. Режимы работы блочных шифров». Об этом в следующих статьях.
Исходный код в виде проекта на Qt
Еще по теме: Режимы шифрования блочных шифров



Можно ли получить ссылку на полный проект на github?
В конце статьи добавил исходный код в виде проекта на Qt.
В проекте массив out_blk объявлен с размером в 4 бата: uint8_t out_blk[4]. Однако внутри функций работа с ним идёт как с 8-и батовым. Как это понимать?